558. Червячные дыры
Червячная дыра – это
односторонний тоннель, соединяющий две звездные системы. Время движения по
тоннелю мгновенно, но при этом можно попасть либо в будущее, либо в прошлое на
определенное число лет. Тоннели соединяют только разные звездные системы.
Известно, что из Солнечной системы можно попасть в любую другую звездную
систему. В задаче необходимо установить, можно ли землянину, двигаясь по
червячным дырам, попасть в бесконечное прошлое.
Вход. Первая строка содержит количество тестов c.
Первая строка каждого теста содержит число звездных систем n (1 £ n £ 1000) и число червячных дыр m (0 £ m £ 2000). Звездные системы нумеруются числами от 0 до n – 1
(Солнечная система имеет номер 0). Следующие m строк содержат три числа x,
y, t (-1000 £ t
£ 1000). При перемещении со звездной системы x в
систему y происходит перемещение во времени на t лет. Если t
> 0, то перемещение происходит в будущее, если t < 0 – то в
прошлое.
Выход. Для
каждого теста вывести сообщение “possible” или “not possible” в зависимости от
возможности ил невозможности попасть в бесконечное прошлое.
Пример входа
2
3 3
0 1 1000
1 2 15
2 1 -42
4 4
0 1 10
1 2 20
2 3 30
3 0 -60
Пример выхода
possible
not possible
РЕШЕНИЕ
графы, циклы отрицательной длины, алгоритм Беллмана - Форда
Анализ алгоритма
Если в графе существует
цикл отрицательной длины, то двигаясь по нем можно попасть в бесконечное
прошлое. Для проверки существования такого цикла следует воспользоваться
алгоритмом Беллмана – Форда.
Обозначим через d[v] верхнюю оценку веса
кратчайшего пути из начальной вершины s в вершину v.
Пусть w(u, v) – вес ребра (u, v). Релаксацией ребра
(u, v) называется уменьшение значения d[v] до d[u]
+ w(u, v) (если второе значение меньше первого).
Relax(u, v, w)
if (d[v] > d[u] + w(u, v))
then d[v] = d[u] + w(u, v);
Изначально следует положить
значения d[v] для всех v Î V(G) \ {s} равными плюс
бесконечности, а d[s] = 0. Это совершается в процедуре инициализации.
инициализация (G, s)
for всех вершин v Î V(G) do d[v] = ¥;
d[s] = 0;
Функция Bellman_Ford совершает релаксацию всех ребер |V(G)| – 1 раз. Если в графе присутствует цикл отрицательной длины, то
по завершению предыдущей операции существует ребро (u, v),
для которого выполняется неравенство d[v] > d[u] + w(u, v). Функция Bellman_Ford возвращает FALSE, если
найден цикл отрицательной длины и TRUE иначе.
Bellman_Ford(G, w, s)
иницализация (G, s)
for i = 1 to |V(G)|
– 1 do
for каждого ребра (u, v) Î E(G) do Relax(u, v, w);
for каждого ребра (u, v) Î E(G) do
if d[v] > d[u] + w(u,
v) then return FALSE;
return TRUE;
Поскольку землянин стартует
с Солнечной системы, то начальной будет вершина с номером 0, то есть s =
0.
Лемма. Пусть d(s, v) –
длина кратчайшего пути от s до v. Пусть G(V, E) – взвешенный
ориентированный граф с весовой функцией w, не содержащий циклов
отрицательного веса, достижимых из s. Тогда по окончании работы
процедуры Bellman_Ford будет выполняться
равенство d[v] = d(s, v) для
всех вершин v, достижимых из s.
Лемма. Если в графе существует
цикл отрицательной длины, то существует ребро (u, v), для которого выполняется
неравенство d[v]
> d[u] + w(u, v).
Доказательство. Пусть (v0,
v1, …, vk = v0) – цикл
отрицательной длины, достижимый из исходной вершины, но при этом d[vi+1]
£ d[vi] +
w(vi, vi+1) для всех i =
0, 1, …, k – 1. Сложив эти k неравенств, и сократив на 
, получим: 0 £ 
. Последнее неравенство противоречит тому что (v0,
v1, …, vk = v0) является
циклом отрицательной длины. Сокращаемая сумма конечна, так как все
вершины vi достижимы.
Пример
Рассмотрим первый
пример. Граф содержит 3 вершины. Проводим два раза релаксацию всех ребер.
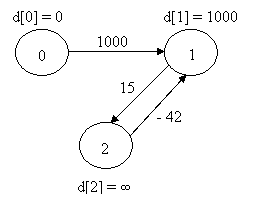
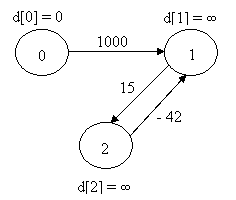
начальное состояние граф после первой
релаксации всех ребер
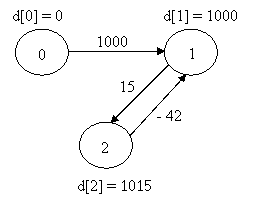
граф после второй
релаксации всех ребер
Для ребра (2, 1) имеет
место неравенство: d[1] > d[2] + w(2, 1) (1000 > 1015 – 42). Значит
существует цикл отрицательной длины, в который входит ребро (2, 1). Таким
циклом будет 1 – 2 – 1 и его величина равна 15 – 42 = -27.
Во втором тесте циклов
отрицательной длины нет.
Реализация алгоритма
Каждая червячная дыра задается своими концами и
временем, на которое она перемещает путника. Номера звездных систем,
являющимися концами i – ой дыры, храним в ячейках массивов x[i]
и y[i], величину перемещения во времени – в w[i].
int x[2001],
y[2001], w[2001];
Функция Bellman_Ford возвращает 0, если в исследуемом
графе есть хотя бы один цикл отрицательной длины, и 1 в противном случае.
Для каждой вершины v значение d[v]
хранит верхнюю оценку веса кратчайшего пути из начальной вершины в вершину v.
Начальной является нулевая вершина, соответствующая Солнечной системе. Положим
в начале работы алгоритма d[0] равным 0, а d[v] равным некоторому
максимально возможному числу (например, 0x3F3F3F3F).
int Bellman_Ford(void)
{
int d[1001], i, j;
memset(d,0x3F,sizeof(d));
d[0] = 0;
Повторим n (по числу вершин в графе) раз
следующую процедуру: для каждого ребра графа произвести его релаксацию. Для
избежания переполнения при сложении d[x[j]] + w[j] следует
удостовериться, что значение d[x[j]] меньше максимального числа.
for(i = 0; i < n; i++)
for (j = 0; j < m; j++)
if (d[x[j]] < 0x3F3F3F3F)
if (d[y[j]] > d[x[j]] + w[j])
d[y[j]] = d[x[j]] + w[j];
Проверим, существует
ли цикл отрицательной длины. Перебираем все ребра (x[j], y[j]), 0
£ j
< m. Если для некоторого j - го ребра выполняется условие d[y[j]]
> d[x[j]] + w[j], то обнаружен цикл отрицательной длины.
Возвращаем 0 и выходим из функции.
for(j = 0; j < m; j++)
if (d[y[j]]
> d[x[j]] + w[j]) return 0;
Циклов отрицательной длины не найдено. Возвращаем 1.
return 1;
}
Основная процедура. Читаем число тестов k. Для
каждого теста вводим число звездных систем n и число червячных дыр m.
Далее читаем информацию о тоннелях в массивы x, y, w.
scanf("%d",&k);
while (k--)
{
scanf("%d %d",&n,&m);
for(i = 0; i < m; i++)
scanf("%d
%d %d",&x[i],&y[i],&w[i]);
Запускаем функцию Bellman_Ford. В зависимости от ее
результата выводим информацию о возможности или невозможности переместиться в
минус бесконечность.
if (Bellman_Ford()) printf("not
");
printf("possible\n");
}